基于模型索引图生成植被与渲染的方案

Posted on | In | | Visitors

　　欢迎参与讨论，转载请注明出处。

前言

0
　　看着这光秃秃草地，这不整点草上去像样么？之前采用的放置若干草堆装饰物点缀，效果实在捉急。于是这波决定采取GPU Instance在草地上都填满草，这可以说是PS4时代下半场以来的标配了：
1
　　若是按照传统工作流，也许就是什么刷草编辑器走起了。可惜我们并没有这个人力去做这种事情，且对于草的放置需求也很明确：在草地及其周边铺满，并加上一定的疏密变化即可。恰好我们的地形渲染也是自制的，对于草地的所在实际上是有索引贴图控制的：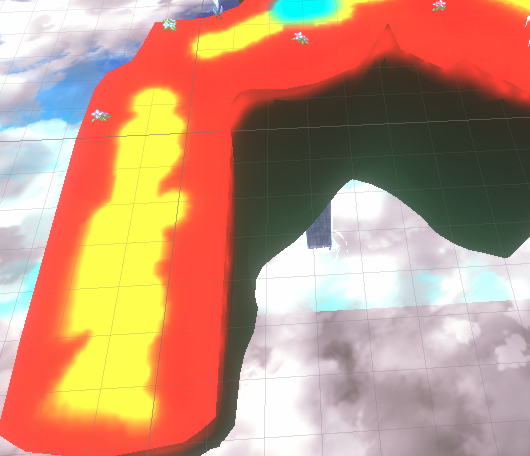
2
　　如上图所示，红色的部分即是草地，那么事情就变得明了了：只要能获取到贴图红色部分的坐标等信息，转换一番不就能给GPU Instance使用了？事不宜迟，这就开干！

索引图转换

　　在正式开动之前还需要注意一个问题：不是给草地硬生生的填满了草就完事的，需要具有一定的疏密变化，且草地与其他地块之间的过渡处也要多少有点草，不然搞得跟防火带似得。由此可见，直接使用地形的索引贴图并非是个好的选择。于是我选择开发了转换工具：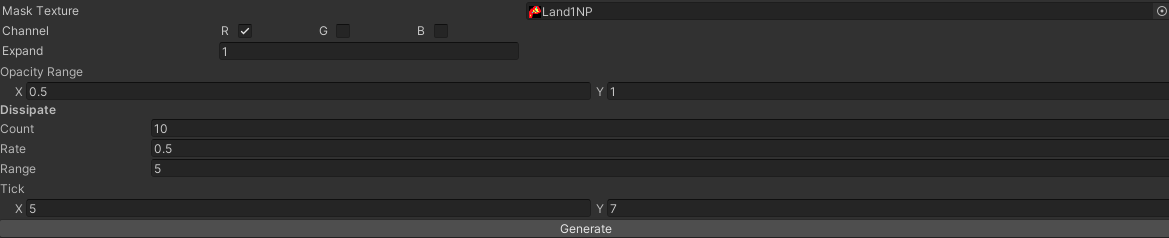
3
　　最后导出为黑白图：
4
　　其功能大致为：

  • 指定转换通道(Channel)
  • 通道外扩（Expand）
  • 通道值随机（Opacity Rate）
  • 随机选择位置展开挖孔（Dissipate）

　　如此较之地形索引图，便有了更多的变化了。

三角面填充

　　有了转换后的索引图，接下来便是生成了。根据uv采样贴图，得到模型对应的位置在Shader里倒是相当简单。可在CPU端进行则需多费一番功夫了：我们知道模型是由多个三角面组成，每个三角面对应三个顶点，每个顶点有着自己的坐标、法线、UV等信息。但问题在于我们无法直接获得三角面内部的这些信息，而这在Shader里是经过光栅化后所以才能取得的。换言之，我们需要自己整个软光栅。
　　这软光栅听着玄乎，实际上在这里只是用一个单位值，在三角形内部步进，得到一系列的点罢了，详细算法可以参考市面上的三角形填充算法，其原理并非本文内容，不作复述。
　　在获得了三角面内部的一个个点后，我们还需要得到它们的坐标、法线、UV等信息。这需要获取该点相对于三角面的三个顶点的距离权重，将相关信息插值得出。如何取得这个距离权重，这便又引申出另一个算法：三角形线性插值。这其实便是实现软渲染的必备一环，这俩算法组合拳便能得出这个经典的RGB插值三角形了：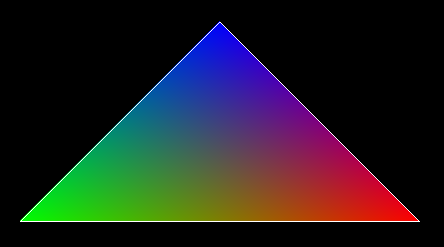
5

多线程生成

　　有了三角面填充坐标点后，便可考虑生成的事了，首先要明确生成的策略：

  • 根据填充单位值对模型的三角面生成若干点，每个点都会记录相应信息（坐标、法线、UV、通道值），通道值根据UV采样贴图而得
  • 另外会根据点的法线值检查所在角度是否合法（不希望墙壁之类的地方也生成），对于角度不合法的点会作废处理
  • 根据合法点的通道值累加，除以一个可配置的系数，决定该模型能填充的草数量（草数量 = 总通道值 / 系数）
  • 在总数量的前提下，随机挑选合法点种草，最后将草数据导出即可

　　按照这套逻辑直接开干自然是没毛病，但性能这块实在捉急（模型的三角面太多、三角形填充以及贴图采样都耗时），然而这其实是个很适合并行化的作业（以三角面为单位），以及最后的草随机生成。那么便可引入JobSystem搞事了，整个工作流将会变成：

  • 配置模型及其转换后的索引贴图，配置相关生成参数（填充单位值、系数等）
  • 收集点信息：创建CollectJob，将相关数据传入（三角面、顶点、UV集合等），以模型三角面数为作业量，对每个三角面填充点，筛选掉不合法的点，导出到统一容器中
  • 遍历容器成员，将每个作业的成果导入到外部容器中
  • 生成草信息：创建GenerateJob，将相关数据传入（点集合、模型矩阵、随机算子等），以草生成数为作业量，随机选择点进行草数据的生成
  • 将草信息容器转换为数组导出

　　需要注意的是，JobSystem只支持非托管类型资源。也就是说我们不能直接将诸如Mesh、Texture2D之类的资源直接传入使用，得做点转换工作：

1
2
3
4
5
6
7
8
var job = new CollectJob();
job.vertices = new NativeArray<Vector3>(mesh.vertices, allocator);
job.uvs = new NativeArray<Vector2>(mesh.uv, allocator);
job.normals = new NativeArray<Vector3>(mesh.normals, allocator);
job.triangles = new NativeArray<int>(mesh.triangles, allocator);
job.maps = new NativeArray<Color>(texture.GetPixels(), allocator);
job.texelSize = new Vector2Int(texture.width, texture.height);

　　是的，就连容器都得使用Unity专门开发的Native Container，不可以用诸如数组、List之流。
　　另外对于CollectJob的点数据导出，经过我的一番实践，想要在多个作业同时导出到同一个容器，并且没有冲突的话，最佳方式是创建一个NativeArray对象，为每个作业开辟一定的空间，保证每个作业之间的写入区域是相互独立的：

1
2
3
4
5
var job = new CollectJob();
// length代表作业数，TRIANGLE_MAX表示每个三角形的最大可填充数量
job.points = new NativeArray<Point>(length * TRIANGLE_MAX, allocator, NativeArrayOptions.UninitializedMemory);
job.counts = new NativeArray<int>(length, allocator); // counts记录每个作业的填充数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// i, j, k表示三角面对应的三个顶点索引
var p1 = new Vector2(this.vertices[i].x, this.vertices[i].z);
var p2 = new Vector2(this.vertices[j].x, this.vertices[j].z);
var p3 = new Vector2(this.vertices[k].x, this.vertices[k].z);
// 填充三角面
NativeList<Vector2> vertices = Triangles.FillTriangle(p1, p2, p3, this.precision);
this.counts[index] = 0;
// 遍历顶点，构建点数据
for (int n = 0; n < vertices.Length; n++) {
    // 超出上限则取消
    if (this.counts[index] > TRIANGLE_MAX) {
        break;
    }
    
    // 获取相对三个顶点的距离权重
    Vector3 rates = Triangles.GetTriangleRates(vertices[n], p1, p2, p3);
    
    // 根据距离权重，获取点各项数据
    Vector3 position = this.vertices[i] * rates[0] + this.vertices[j] * rates[1] + this.vertices[k] * rates[2];
    Vector2 uv = this.uvs[i] * rates.x + this.uvs[j] * rates.y + this.uvs[k] * rates.z;
    Vector3 normal = this.normals[i] * rates.x + this.normals[j] * rates.y + this.normals[k] * rates.z;
    float weight = this.SampleTexture(uv);
    float angle = Vector3.Angle(Vector3.up, normal);
    // 拥有通道值且角度合法的点方可加入
    if (weight > 0 && math.abs(angle) < this.angleMax) {
        // 保证各作业的写入位置是独立的
        var point = new Point() {position = position, uv = uv, normal = normal, weight = weight + weight * weight};
        this.points[index * TRIANGLE_MAX + this.counts[index]] = point;
        this.counts[index]++;
    }
}

　　如此最后便可将容器内的数据导出到外部容器了：

1
2
3
4
5
6
7
8
9
10
11
12
private List<Point> PackPoints(in NativeArray<Point> points, in NativeArray<int> counts) {
    var list = new List<Point>();
    
    for (int i = 0; i < counts.Length; i++) {
        for (int j = 0; j < counts[i]; j++) {
            var point = points[i * TRIANGLE_MAX + j];
            list.Add(point);
        }
    }
    return list;
}

　　生成草数据部分的GenerateJob则更为简单，由于它的生成数量是一开始便定好的，所以构造作业量长度的容器即可：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
float weight = 0;
// 取得总通道值
foreach (var point in points) {
    weight += point.weight;
}
// 获取生成数量
int count = (int)(weight / group.opacity);
count = count > points.Count ? points.Count : count;
var job = new GenerateJob();
job.units = new NativeArray<Unit>(count, allocator);
job.points = points.ToNativeArray(allocator);
// 草坐标与模型矩阵有关
job.matrix = group.gameObject.transform.localToWorldMatrix;
// Job内使用的随机数需要来自Unity.Mathematics
job.random = new Random();
job.random.InitState();
var handle = job.Schedule(count, 1);
handle.Complete();
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public void Execute(int index) {
    // 从points随机选择生成unit
    int idx = this.random.NextInt(this.points.Length);
    Point point = this.points[idx];
    this.units[index] = this.NewUnit(point);
}
private Unit NewUnit(in Point point) {
    // 构建矩阵，与模型矩阵结合，获得正确的坐标点
    var matrix = new Matrix4x4();
    matrix.SetTRS(point.position, Quaternion.identity, Vector3.one);
    matrix = this.matrix * matrix;
    // 为了节省内存，草的数据实际上只有坐标，其余部分在Shader随机生成
    var unit = new Unit() {
        position = new Vector3(matrix.m03, matrix.m13, matrix.m23)
    };
    return unit;
}

渲染支持

　　有了数据之后，接下来便是将它们渲染出来了：我们会使用一个MonoBehavior，在LateUpdate时调用Graphics.DrawMeshInstancedIndirect进行草的批量绘制。为此需要两个关键的Compute Buffer：argsBuffer与unitBuffer，一者作为绘制API的参数，提供绘制模型的相关信息以及数量。另者即是草的数据集封装，传入材质属性供Shader使用：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
[ExecuteAlways]
public class GrassSolution : MonoBehaviour {
    [Serializable]
    public struct Unit {
        public Vector3 position;
    }
    public Mesh mesh;
    public Material material;
    private ComputeBuffer argsBuffer;
    private ComputeBuffer unitBuffer;
    private void InitUnits() {
        // ComputeBuffer的核心数据属于非托管资源，需要手动释放
        if (this.unitBuffer != null) {
            this.unitBuffer.Release();
        }
        // 将草数据集传入
        this.unitBuffer = new ComputeBuffer(this.units.Length, sizeof(Unit));
        this.unitBuffer.SetData(this.units);
    }
    private void InitArgs() {
        // 构建所需参数
        var args = new uint[] {
            this.mesh.GetIndexCount(0),
            (uint)this.units.Length,
            this.mesh.GetIndexStart(0),
            this.mesh.GetBaseVertex(0),
            0
        };
        if (this.argsBuffer != null) {
            this.argsBuffer.Release();
        }
        // 传入参数信息
        this.argsBuffer = new ComputeBuffer(1, sizeof(uint) * 5, ComputeBufferType.IndirectArguments);
        this.argsBuffer.SetData(args);
    }
    protected void Start() {
        // 初始化ComputeBuffer
        this.InitUnits();
        this.InitArgs();
        // 将unitBuffer数据传入Shader
        this.material.SetBuffer("_Units", this.unitBuffer);
    }
    protected void LateUpdate() {
        // 指定模型与材质，每帧绘制
        Graphics.DrawMeshInstancedIndirect(this.mesh, 0, this.material, this.bounds, this.argsBuffer);
    }
}

　　到了Shader层面，还需要对接草的坐标信息，才能渲染到正确的位置：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 定义草的数据结构
struct Unit
{
    float3 position;
};
// ComputeBuffer容器，对应this.unitBuffer
StructuredBuffer<Unit> _Units;
Varyings Vert(Attributes input, uint instanceID : SV_InstanceID)
{
    // 根据instanceID获取对应的草数据
    Unit unit = _Units[instanceID];
    // 赋予坐标
    input.positionOS.xyz += unit.position;
    // ...
}

视矩剔除

　　如此一来草的渲染自然不是问题了：
6
　　但可以看到，整个场景一眼望去，草的数量还是不少的。并且在视野内能看到的充其量就一个地块而已，为了保证性能，还需要引入视矩剔除。
　　本方案采取的视矩剔除方案相当简单：在空间中根据草所在之处划分出一个个格子，每个格子记录所包含草的索引集以及格子的中心坐标，就像这样：
7
　　格子的生成可在先前的草数据生成后再追加一步：遍历草坐标，将其划分到对应的格子对象中，将格子数据也一并导出即可。但仅此而已还不够完美：这样需要让格子对象存储所辖草的索引集，数据量较大。所以我们可以先将草数据分类到不同的格子容器中，最后将格子容器的草数据一一重写回草的容器中，以此确保每个格子所辖的草索引是连续的，如此只需要为每个格子记录索引起始值以及数量即可：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
private List<Cell> GenerateCells(List<Unit> units) {
    var unitsMap = new Dictionary<Vector3Int, List<Unit>>();
    // 将每根草划分到对应的格子容器中
    foreach (var unit in units) {
        var pos = unit.position;
        var cellPos = ToCellPos(pos);
        if (!unitsMap.ContainsKey(cellPos)) {
            unitsMap.Add(cellPos, new List<Unit>());
        }
        unitsMap[cellPos].Add(unit);
    }
    // 清空草容器
    units.Clear();
    // 根据格子容器将草重新写回草容器中
    foreach (var iter in unitsMap) {
        foreach (var unit in iter.Value) {
            units.Add(unit);
        }
    }
    // 构建格子数据集
    var cells = new List<Cell>();
    var count = 0;
    // 构建格子数据，记录格子的草索引起始、数量、格子中心坐标
    foreach (var iter in unitsMap) {
        var cell = new Cell() {
            center = ToCellCenter(iter.Key),
            begin = count,
            count = iter.Value.Count
        };
        cells.Add(cell);
        count += iter.Value.Count;
    }
    return cells;
}

　　有了数据之后，接下来便是剔除了：

  • 构建格子的ComputeBuffer（cellBuffer），以及构建一个存储草的可视索引集ComputeBuffer(visibleIdBuffer)
  • 编写ComputeShader，以格子数量为作业量，判断每个格子是否在摄像机视矩体内，若存在则将格子所辖的草索引传入visibleIdBuffer中
  • Compute Shader运行完毕后，将visibleIdBuffer的成员数通过ComputeBuffer.CopyCount传入argsBuffer的第二项（用于控制渲染数量）
  • 最后在Shader通过visibleIdBuffer[instanceID]获取草的索引值，由此间接取得草的数据
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
[Serializable]
public struct Cell {
    public Vector3 center;
    public int begin;
    public int count;
}
// 构建cellBuffer
private void InitCells() {
    if (this.cellBuffer != null) {
        this.cellBuffer.Release();
    }
    this.cellBuffer = new ComputeBuffer(this.cells.Length, sizeof(Cell));
    this.cellBuffer.SetData(this.cells);
}
// 构建visibleIdBuffer
private void InitVisbleId() {
    if (this.visibleIdBuffer != null) {
        this.visibleIdBuffer.Release();
    }
    // 它的最大长度为草数据的长度，ComputeBufferType.Append表明它是个可填充容器
    this.visibleIdBuffer = new ComputeBuffer(this.units.Length, sizeof(int), ComputeBufferType.Append);
}
private void Cull() {
    // Compute Shader一次并行32组
    int patch = Mathf.CeilToInt(this.cells.Length / 32.0f);
    // 获得当前视图下的投影矩阵
    var camera = Camera.main;
    var vp = camera.projectionMatrix * camera.worldToCameraMatrix;
    // 清空容器
    this.visibleIdBuffer.SetCounterValue(0);
    // 传递所需数据，开始作业
    this.shader.SetBuffer(id, "_VisibleIds", this.visibleIdBuffer);
    this.shader.SetBuffer(id, "_Cells", this.cellBuffer);
    this.shader.SetInt("_Count", this.cells.Length);
    this.shader.SetMatrix("_VPMatrix", vp);
    this.shader.Dispatch(id, patch, 1, 1);
    // 将visibleIdBuffer的数量传递给argsBuffer，决定渲染数量
    ComputeBuffer.CopyCount(this.visibleIdBuffer, this.argsBuffer, sizeof(uint));
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
// Compute Shader
#pragma kernel CSMain
struct Cell
{
    float3 center;
    int begin;
    int count;
};
StructuredBuffer<Cell> _Cells;
AppendStructuredBuffer<int> _VisibleIds;
float4x4 _VPMatrix;
int _Count;
[numthreads(32, 1, 1)]
void CSMain (uint3 groupID : SV_GroupID, int index : SV_GroupIndex)
{
    // 获取当前作业对应的格子id
    int n = groupID.x * 32 + index;
    // 确保处理的格子是在范围内的
    if (n < _Count)
    {
        // 获取格子中心坐标
        float3 posWS = _Cells[n].center;
        // 将格子坐标转换到裁剪空间
        float4 absPosCS = abs(mul(_VPMatrix, float4(posWS, 1.0)));
        
        float range = absPosCS.w;
        
        // 判断格子坐标是否在视矩体内
        // 由于格子比较大，肯定会有一部分元素在视矩体之外，所以要扩大点范围
        if (absPosCS.x <= range * 1.5 && absPosCS.y <= range * 1.6)
        {
            // 将格子所辖的草索引加入容器中
            for (int i = 0; i < _Cells[n].count; i++) {
                _VisibleIds.Append(_Cells[n].begin + i);
            }
        }
    }
}
1
2
3
4
5
6
7
8
9
10
// Shader
StructuredBuffer<Unit> _Units;
StructuredBuffer<int> _VisibleIds;
Varyings Vert(Attributes input, uint instanceID : SV_InstanceID)
{
    // 间接获得草数据
    int idx = _VisibleIds[instanceID];
    Unit unit = _Units[idx];
}

　　如此，将Cull函数放到适当的场合运行，草的剔除便算完成了：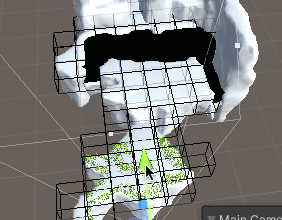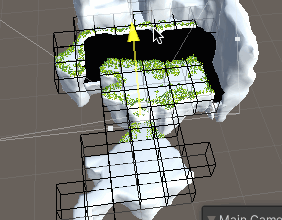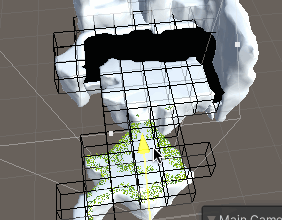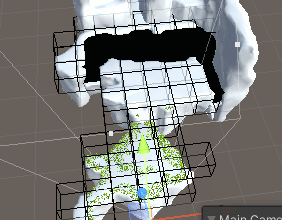
8

渲染效果

　　终于可以聊点开心的东西了，毕竟渲染效果这种东西是最直观的了，直接上效果：
9
　　本方案使用的草属于面片草，它通过一个面片模型，选择若干草的图片，使用AlphaClip剔除透明度进行渲染：
10
　　之所以使用AlphaClip而非正统的2D半透明AlphaBlend，是因为在不写入深度的前提下，Instance渲染的次序需要自己把控。然而在使用了剔除之后还要兼顾排序属实有点麻烦，并且哪怕如此也无法达到像素级别的排序：
11
　　那么只好AlphaClip顶硬上了，这样的缺点是边缘会出现狗牙，连MSAA都救不了：
12
　　当然狗牙也就狗牙了，游戏视角下看起来凑合的话就还好，在不考虑太过风骚的操作下，可通过提升贴图精度以及提高渲染分辨率缓解，就这样吧。
　　渲染的本身部分首当其冲的便是随机的缩放与旋转，以及颜色了。为了节省内存，在CPU端提供的数据只有坐标，其余部分则在Shader内通过随机而成：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
int _ColorMax; // 颜色上限
float2 _ScaleW; // 缩放宽度的范围
float2 _ScaleH; // 缩放高度的范围
float2 _AngleY; // 旋转Y轴的范围
float2 _AngleXZ; // 旋转XZ轴的范围
float4 _Colors[5]; // 颜色数组
// 构建矩阵
float4x4 MakeMatrix(Unit unit, uint instanceID) {
    float3 pos = unit.position;
    // 随机取值
    float scaleW = lerp(_ScaleW.x, _ScaleW.y, Random(float2(pos.x, pos.y)));
    float scaleH = lerp(_ScaleH.x, _ScaleH.y, Random(float2(pos.y, pos.z)));
    float angleY = lerp(_AngleY.x, _AngleY.y, Random(float2(instanceID, pos.z)));
    float angleXZ = lerp(_AngleXZ.x, _AngleXZ.y, Random(float2(pos.x, instanceID)));
    // 确定缩放与旋转，生成矩阵
    float3 scale = float3(scaleW, scaleH, scaleW);
    float3 angle = float3(angleXZ, angleY, angleXZ);
    float4x4 mat = SetTRS(pos, scale, radians(angle));
    return mat;
}
// 随机颜色
float4 GetColor(Unit unit, uint instanceID) {
    float3 pos = unit.position;
    float rate = Random(float2(instanceID, pos.y));
    int index = lerp(0, _ColorMax - 1, rate);
    
    return _Colors[index];
}
Varyings Vert(Attributes input, uint instanceID : SV_InstanceID)
{
    int idx = _VisibleIds[instanceID];
    Unit unit = _Units[idx];
    float4x4 mat = MakeMatrix(unit, idx);
    
    // 实装草的坐标、缩放、旋转、颜色
    input.positionOS.xyz = mul(mat, input.positionOS).xyz;
    output.color = GetColor(unit, idx);
    // ...
}

　　贴图的随机化也是以此类推，贴图使用TextureArray，随机取得一个贴图索引后采样相应贴图。对于随机的算法选择参考各类噪声算法即可。
　　在做完以上工作后也只有初步的样子而已，仍需进一步加料：
13
　　目前的效果还是太平了，我们给它来加个渐变： 

1
2
3
4
5
// 赋予矩阵前的y坐标
float py = input.positionOS.y;
float gradient = lerp(_Gradient.x, _Gradient.y, py);
output.color.rgb = output.color.rgb * gradient;

14
　　这样多少有点意思了，但颜色给人总体到处都是差不多的，缺乏总体变化感，也许在其他做法里会考虑加入一张全局的颜色贴图，但我们做了全局光照，不如……？ 

1
2
3
4
5
6
7
float gradient = lerp(_Gradient.x, _Gradient.y, py);
// 采样GI底部颜色
float3 gi = GIBottom(vertexInput.positionWS);
// 控制GI颜色比例
output.color = float4(lerp(output.color.rgb, gi, 0.25) * gradient, 1);

15
　　不错不错，而且出于草的位置关系以及性能考虑，我们只需要采样AmbientCube的底部方向的颜色即可。可谓一次有机的结合了。

后记

　　本方案实际仍有不少细节，限于篇幅，只能写到这里了。这应是我有史以来写的最长的一篇文章了吧，但实在是不想拆成多篇来写了。本文限于篇幅，诸多细节未能列出，纯当外行看个热闹，内行看点门道吧。